Дерево решений
В начале XX в. многие американские фермеры увлекались игрой в "15", за решение которой предлагался весьма солидный приз. На квадратном поле размером 4x4 размещались 15 фишек с числовыми номерами 1, 2, ..., 15.
Наличие одного свободного поля позволяло передвигать фишки по горизонтали и вертикали с целью их сортировки по возрастанию номеров. Позиция, за которую предлагалось вознаграждение в размере $100000, содержала единственное нарушение порядка — фишки с номерами 14 и 15 были переставлены местами. Позднее было доказано, что из этой позиции невозможно перейти к полностью упорядоченной последовательности фишек. Так что призовой комитет ничем не рисковал.
Более того, оказалось, что все позиции фишек делятся на две категории. Если суммарное количество нарушений порядка в исходной позиции было четным, то полная сортировка фишек возможна. И тогда единственный смысл игры (исключая простое времяпрепровождение) заключался в достижении полностью упорядоченной расстановки за минимальное количество ходов. Для определенности под ходом мы будем подразумевать перемещение одной фишки на свободное место (в реальной игре прибегают к одновременному сдвигу двух или трех фишек, расположенных в одной строке или одном столбце).
С целью сокращения количества переборов мы продемонстрируем аналогичную игру на поле размером 2x3, где расположены фишки с буквами А, В, С, I, S. Цель игры — за минимальное число ходов перевести заданную исходную позицию в позицию BASIC:
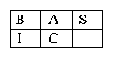
Идея решения этой задачи заключается в построении полного дерева решений, в верхушке которого располагается целевая позиция BASIC. Каждый последующий уровень дерева образуют позиции, полученные из предыдущей вершины за один ход. С целью удобства ввода начальной позиции и последующего отображения ходов пустая клетка у нас будет представлена символом "*".
В нашей игре начало дерева может выглядеть следующим образом:
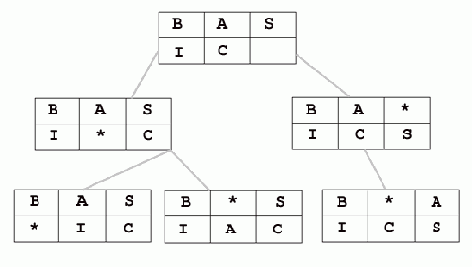
Естественно, что в очередной вершине дерева должна находиться позиция, не повторяющая предыдущие позиции. Так как общее количество перестановок из шести элементов равно 6!=720, то общее количество вершин в нашем дереве не будет превосходить эту границу. Более того, задача симметрична и из целевой позиции BASIC* можно будет породить ровно 359 новых вершин.
Для хранения дерева допустимых позиций используем два массива — массив строк tree, обеспечивающий хранение 360 шестисимвольных значений позиций, и числовой массив ind[360], в элементах которого будут фиксироваться индексы породивших строк. В нашем примере начальное заполнение массивов tree и ind может выглядеть следующим образом (табл. 6.1):
Таблица 6.1. Начальное заполнение массивов tree и ind
|
Индекс строки |
Значение строки |
Ссылка на породившую строку |
||
|
0 |
BASIC* |
-1 |
||
|
1 |
BAIC*S |
0 |
||
|
2 |
BASI*C |
0 |
||
|
3 |
B*AICS |
1 |
||
|
4 |
B*SIAC |
2 |
||
|
5 |
BASIC |
2 |
||
|
6 |
BCAI*S |
3 |
||
И это построение надо продолжать до тех пор, пока мы не встретим целевую вершину, у которой нет продолжения (ее индекс равен —1).
Совет 1 (общий)
Совет 2 (общий)
k = i * 3 + j. i = k div 3. j = k mod 3.
Следует не забывать, что приведенные формулы справедливы, если индексы в массивах отсчитываются от 0, например так, как это делается в Си. Однако в строках Бейсика и Паскаля индексы символов отсчитываются от 1. Поэтому в соответствующих фрагментах программ введена соответствующая коррекция значения одномерного индекса k.
Совет 3 (общий)
Программа 6_01.bas
DECLARE SUB change (il AS INTEGER, j1 AS INTEGER)
DECLARE SUB printTAB (s AS STRING)
DECLARE SUB level ()
DECLARE SUB poisk ()
REM Дерево решений BASIC
DEFINT A-Z
DIM SHARED x0 AS INTEGER, y0 AS INTEGER, nmax AS INTEGER, k AS INTEGER
DIM SHARED from AS INTEGER
DIM SHARED tree(360) AS STRING * 6, ind(360) AS INTEGER, pos0 AS STRING * 6
nmax = 1: x0 = 1: y0 -= 2
tree(0) = "BASIC*"
ind(0) = -1
CLS
INPUT "Введите строку с исходной позицией - ", pos0
FOR from = 0 TO nmax - 1:
level NEXT from poisk END
SUB change (il AS INTEGER, jl AS INTEGER)
DIM n AS INTEGER, kl AS INTEGER, tmp AS STRING, str2 AS STRING
IF (il < 0) OR (il > 1) OR (jl < 0) OR (jl > 2) THEN EXIT SUB
kl = il * 3 + jl + 1
str2 = tree(from)
tmp = MID$(str2, k, 1)
MID$(str2, k, 1) =MID$(str2, kl, 1)
MID$(str2, kl, 1) = tmp
FOR n = 0 TO nmax - 1
IF str2 = tree(n) THEN EXIT SUB
NEXT n
ind(nmax) = from
tree(nmax) = str2
nmax = nmax + 1 END SUB
SUB level
FOR k = 1 TO 6
IF MID$(tree(from), k, 1) = "*" THEN EXIT FOR
NEXT k
i = (k - 1} \ 3 ' номер строки
j = (k - 1) MOD 3' номер столбца
CALL change(i - 1, j)
CALL change(i + 1, j )
CALL change(i, j - 1)
CALL change(i, j + 1)
END SUB
SUB poisk
FOR q = 0 TO nmax - 1
IF pos0 = tree(q) THEN GOTO m
NEXT q
PRINT "Эта позиция не сводится к требуемой"
EXIT SUB
m:
CALL printTAB(tree(q))
q = ind(q)
IF q >= 0 THEN GOTO m
END SUB
SUB printTAB (s AS STRING)
LOCATE y0, x0: PRINT "+-+-+-+"
LOCATE y0 + 1, x0: PRINT " | ";
MID$(s, 1, 1);
PRINT "|"; MID$(s, 2, 1);
PRINT "|"; MID$(s, 3, 1); "I" LOCATE y0 + 2, x0:
PRINT "+-+-+-+" LOCATE y0 + 3, x0: PRINT "|"; MID$(s, 4, 1);
PRINT "|"; MID$(s, 5, 1);
PRINT "|"; MID$(s, 6, 1); " |" LOCATE y0 + 4, x0:
PRINT "+-+-+-+" x0 = x0 + 10
IF x0 = 81 THEN y0 = y0 + 5: x0 = 1
END SUB
Программа 6_01.с
#include <stdio.h>
#include <conio.h>
#include <string.h>
void level();
void change(int il, int J12);
void poisk(};
void print_tab(char* s);
char tree[360][7];
char pos0[7];
int ind[360];
int i,j,k,nmax=l;
int x0=l,y0=2;
int from;
void main() {
strcpy(&tree[0][0],"BASIC*");
ind[0]=-l;
clrscr();
printf("Введите строку с исходной позицией - ");
scanf("%s",pos0);
for(from=0; from<nmax; from++) level();
poisk () ;
getch ();
}
//---------------------------------
void level() {
for{k=0; k<6; k++)
if(tree[from][k]=='*')break;
i=k/3; //номер строки
j=k%3; //номер столбца
change (i-1,j);
change(i+1,j);
change(i,j-1);
change(i,j+1); }
//-------------------------------------
void change(int i1, int j1) { char tmp,str2[7];
int n,kl;
if(il<0 || i1>l || jl<0 | | jl>2) return;
kl=il*3+jl;
strcpy(str2, (char*)street from][0]);
tmp=str2[k]; str2[k]=str2[kl]; str2[kl]=tmp;
for(n=0; n<nmax; n++)
if(strcmp(str2,(char*)&tree[n][0])==0) return;
ind[nmax] =f rom;
strcpy((char*)stree[n] [0] , str2);
nmax++;
}
//--------------------------------------
void poisk() { char *p;
p=Stree[0][0] ;
for(int q=0; q<nmax; q++)
if(strcmp(pos0,p+q*7)==0) goto m;
printf("\ n Эта позиция не сводится к требуемой");
return;
m:
print_tab(p+q*7) ;
q=ind[q];
if(q>=0) goto m;
return;
}
//-------------------------------------------
void print_tab(char* s) { char top[]= "+-+-+-+";
charmid[]= "+-+-+-+";
char bottom[]="+-+-+-+";
gotoxy(x0,y0);
printf("%s",top);
gotoxy(x0,y0+l) ;
printf("|%c|%c!%c|",s [0],s [1],s [2]);
gotoxy(x0,y0+2);
printf("%s", mid);
gotoxy(x0,y0+3);
printf(";%ci%ci%c!",s[3],s[4],s[5]);
gotoxy(x0,y0+4);
printf("%s",bottom);
x0=x0+10;
if(x0==81){y0=y0+5;x0=l;} }
Программа 6_01.pas
program basic; uses Crt;
var
tree:array [0..359] of string[6];
pos0:string[6];
ind:array [0..359] of integer;
x0,y0,i,j,k,nmax,from:integer;
procedure print_tab(s:string);
begin
gotoxy(x0,y0);
write{'+-+-+-+' );
gotoxy(x0,y0+1);
write {' |',s[l],'|',s[2],'|',s[3],'|');
gotoxy(x0,y0+2);
write('|-+-+-|');
gotoxy(x0,y0+3);
write('!',s[4],'|',s[5],'|',s[6],'| ');
gotoxy(x0,y0+4);
write('+-+-+-+');
x0:=x0+10;
if(x0=81)then begin y0:=y0+5;
x0:=l;
end;
end;
procedure poisk;
var
q:integer;
label m; begin
for q:=0 to nmax-1 do
if pos0=tree[q] then goto m;
write(' Эта позиция не сводится к требуемой');
readln;
exit;
m:
print_tab(tree[q]};
q:=ind[q];
if q>=0 then goto m;
end;
procedure change(il,jl:integer);
var
tmp:char;
str2:string[6];
n,kl:integer; begin
if (i1<0)or (i1>l)or(j1<0)or(j1>2) then exit;
kl:=il*3+jl+l;
str2 : =tree.[ from] ;
tmp:=str2[k] ;
str2[k]:=str2[kl];
str2[kl]:=tmp;
for n:=0 to nmax-1 do
if str2=tree[n] then exit;
ind[nmax]:=from;
tree[nmax]:=str2;
inc(nmax); end;
procedure level; begin
for k:=l to 6 do
if tree[from] [k] = '*' then break;
i:=(k-l) div 3; {номер строки}
j:=(k-l) mod 3; {номер столбца}
change(i-1,j};
change(i+1,j);
change(i,j-1);
change(i,j+1);
end;
begin
nmax:=l;
x0:=l; y0:=2;
tree[0]:='BASIC*';
ind[0]:=-1;
clrscr;
write('Введите строку с исходной позицией');
read(pos0);
for from:=0 to 359 do level;
poisk;
readln;
end.